Compensation Theorem | Introduction, Need, and Advantages

Introduction

To understand the compensation theorem let’s, imagine you have a network or circuit with different parts (branches) connected to it. When something changes, like the resistance in one of these parts, it affects how much voltage and current flow through that specific part of the network.

Now, think about Ohm’s law, which says that when electricity moves through something like a resistor, it causes a voltage drop. This drop in voltage kind of pushes against the voltage from the power source.

To deal with this, we use the compensation theorem. It’s like a solution that helps us manage these changes. Here’s how it works: If there’s a change in a part of the circuit, we add an extra voltage source. This new source has the opposite direction of the main source (like a mirror image), and its strength matches the voltage drop caused by the change.

So, the compensation theorem helps us deal with changes by adding this “opposite” voltage to balance out the effects of the change, making sure the circuit keeps working smoothly.

What is the Compensation Theorem?

In a network, when electricity moves through a resistor (which resists the flow), it causes a voltage drop. The compensation theorem says that instead of using that resistor, we can put in a special voltage source that has no resistance itself. This special source mimics the voltage drop that happened across the resistor due to the current flowing through it.

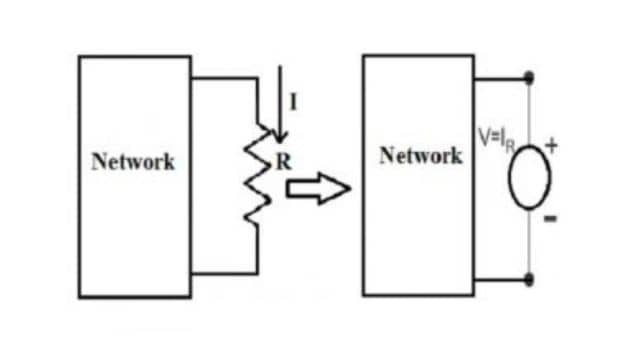
This new source is like a counter-voltage that pushes back against the original voltage or current direction. It’s a way to swap out the resistor for something that behaves like the voltage drop without actually using a resistor. This helps us understand and work with the network more easily.

Explanation:

Let us assume a load RL be connected to a DC source network whose Thevenin’s equivalent gives V0 as the Thevenin’s voltage and RTH as the Thevenin’s resistance as shown in the figure below:

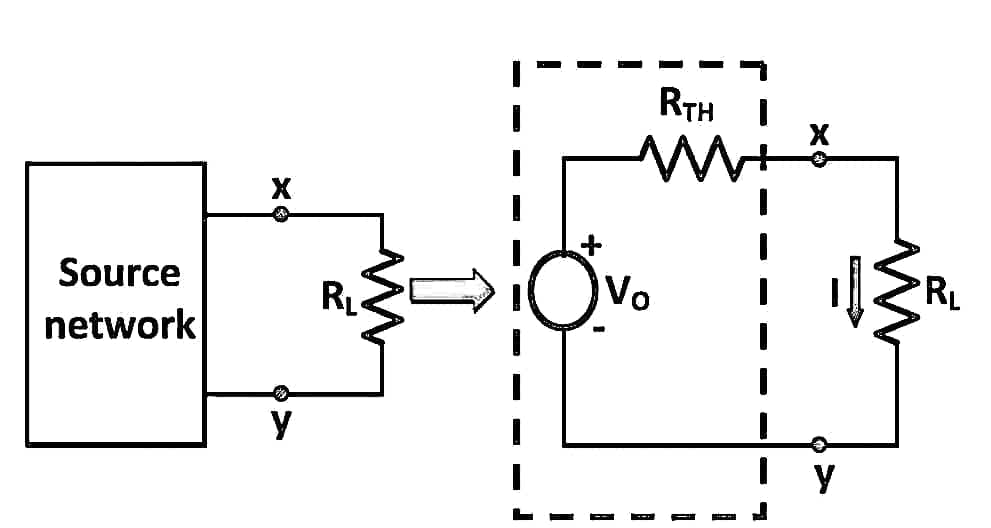
Here,

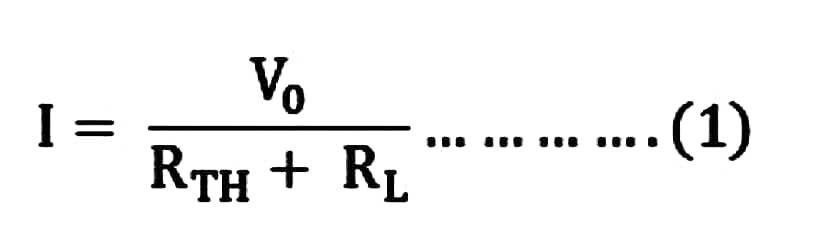
Let the load resistance RL be changed to (RL + ΔRL). Since the rest of the circuit remains unchanged, Thevenin’s equivalent network remains the same as shown in the circuit diagram below:

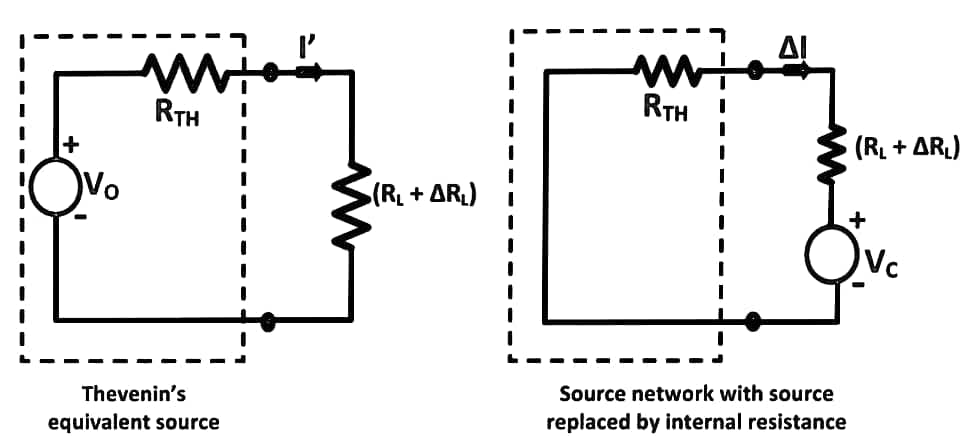
Here,

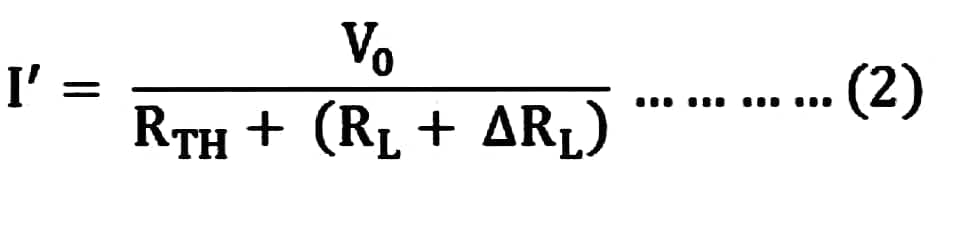
The change of current is termed ΔI

Therefore,

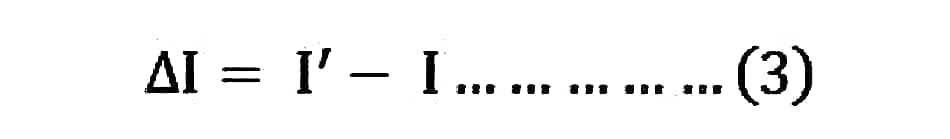
Putting the value of I’ and I from the equation (1) and (2) in the equation (3) we will get the following equation:

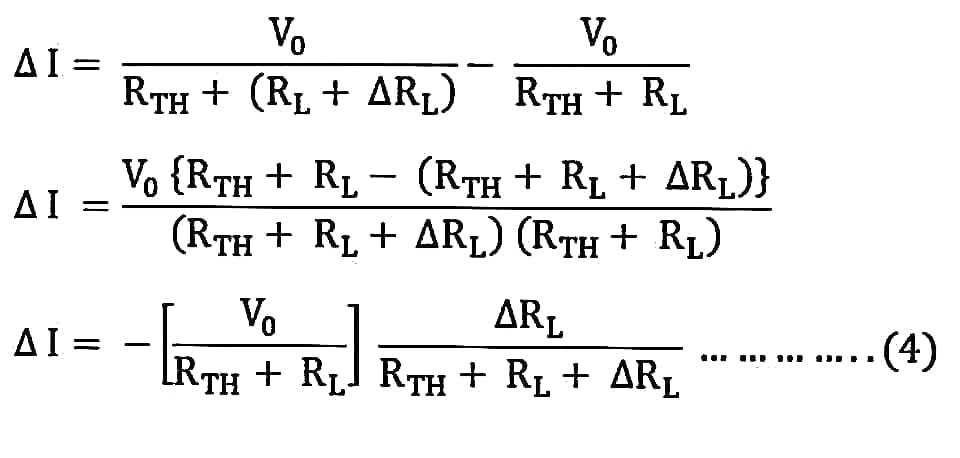
Now, putting the value of I from the equation (1) in equation (4), we will get the following equation:

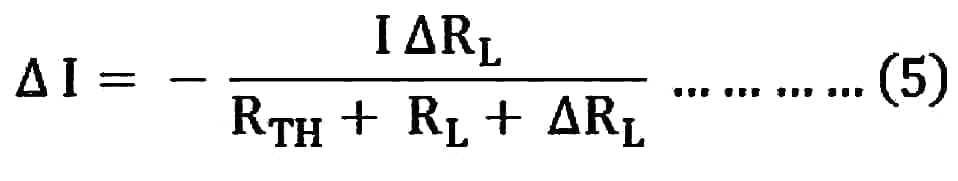
As we know, VC = I ΔRL and is known as compensating voltage.

Therefore, equation (5) becomes,

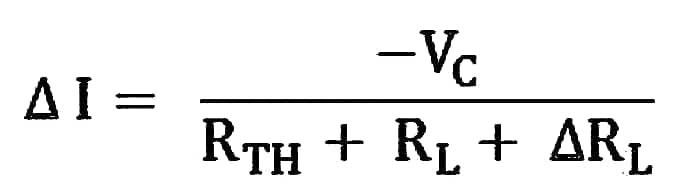
Hence, the Compensation theorem tells that with the change of branch resistance, branch currents change and the change is equivalent to an ideal compensating voltage source in series with the branch opposing the original current, where all other sources in the network are replaced by their internal resistances.

Example of Compensation Theorem

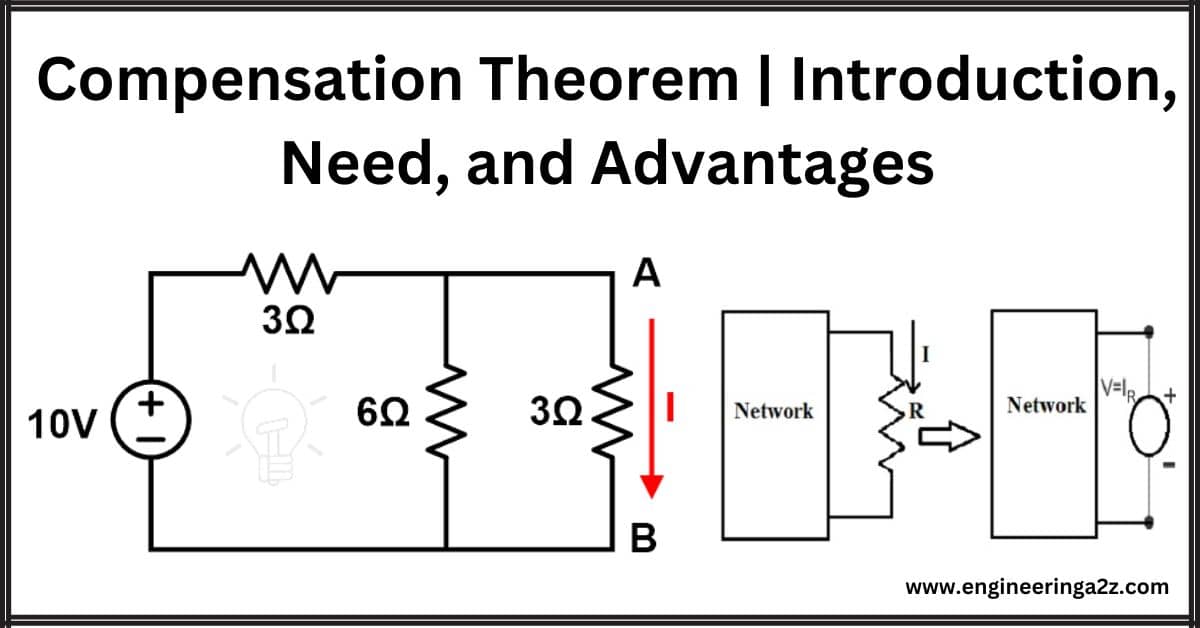
Find the current passing through the branch AB using the compensation theorem when the 3Ω resistance is changed to 9Ω.

Solution:

We need to replace the 3Ω resister with a 9Ω resister. According to the compensation theorem, we need to add a new voltage source in series with the 9Ω resister. The value of this voltage source is;

V_c = I’ ΔZ

Where,

ΔZ = 9 – 3 = 6 Ω and I’ = 4/3 A (or 1.333 A)

V_c = (4/3A) x 6 Ω

V_c = 8 V

A modified circuit diagram or compensated circuit diagram is as shown in the below figure.

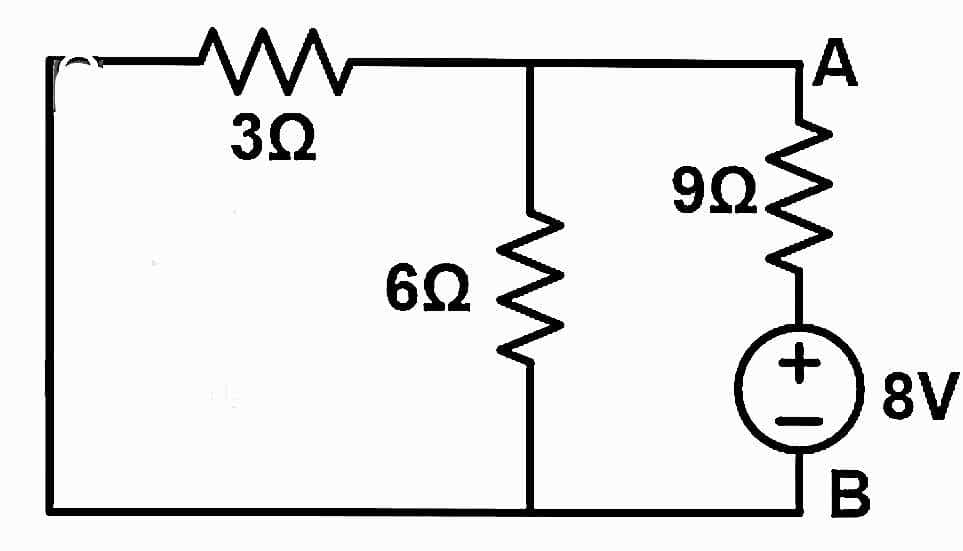
Now, we will find the equivalent resistance. Here, 3Ω and 6Ω resistors are connected in parallel. This parallel combination is connected in series with a 9Ω resister.

R_Eq = 3 | | 6 + 9

Equation 5

R_Eq = 2 + 9

R_Eq = 11 Ω

Now, according to Ohm’s law;

V = ΔI R

8 = ΔI (11 Ω)

ΔI = 8 ÷ 11

ΔI = 0.7272 A

So, according to the compensation theorem; the change in current is 0.7272A.

Need of Compensation Theorem

1. Insightful Network Analysis: The compensation theorem is invaluable as it reveals how changes impact a network. It simplifies finding precise current values in any branch after swapping the network due to a specific alteration in one go.
2. Predictive Precision: Leveraging this theorem, we estimate the impact of even tiny shifts in network components. It’s a powerful way to foresee how minute changes influence the network’s behavior, giving us a glimpse into the effects of these alterations on current flow.

Advantages of Compensation Theorem

1. Insightful Network Changes: The compensation theorem sheds light on how a network transforms when something changes.
2. Built on Ohm’s Law: This theorem operates on the fundamental principle of Ohm’s law, the foundation of electrical relationships.
3. Revealing Voltage and Current Shifts: It assists in uncovering alterations in voltage or current when the resistance in the circuit is tweaked.

Applications of the Compensation Theorem

1. Detecting Small Changes: It’s frequently applied to estimate how tiny adjustments affect electrical network components.
2. Key in Bridge Network Analysis: Particularly valuable for scrutinizing the sensitivity of bridge networks, providing vital insights.
3. Adaptable for Varied Networks: Used extensively to scrutinize networks where component values shift, also exploring the impact of tolerance on these values.
4. Swift Determination of Currents: Allows quick identification of accurate current values in any networked branch by instantly substituting the network due to specific changes.
5. Significant in Network Calculations: This theorem reigns supreme in network analysis, serving as a primary tool to calculate network sensitivity, resolve electrical networks, and comprehend bridge circuits.

Frequently Asked Questions (FAQs)

Read Also:

• Circuit Theorem | Thevenin’s Theorem
• Economics For Engineers Book PDF
• B.Tech – MDU Previous Year Question Papers Download
• Physical Sensors | Classification, Types, and Advantages

Read More>>>>