Table of Contents
Introduction
The Wheatstone Bridge is a gadget invented in 1842 by scientist Wheatstone to figure out how resistant a material is to electricity. It works like a puzzle solver for electrical resistance. Using Kirchhoff’s laws, we can prove the formula behind it.
In simple terms, the Wheatstone Bridge is an electric circuit that helps us measure an unknown resistance by balancing points on a bridge. It’s a cool way to find out how much something resists the flow of electricity.
What is Wheatstone Bridge?
The Wheatstone Bridge is like a smart circuit that helps us figure out the resistance of something unknown. It does this by creating a balanced situation, like a perfectly level seesaw. The circuit has two resistors with known resistance, one mysterious resistor we want to find out about, and a special adjustable resistor.
When we fiddle with the adjustable resistor and get the bridge perfectly balanced, it tells us the resistance of the mystery resistor. It’s like solving an electrical puzzle to accurately measure resistance.
Construction of Wheatstone Bridge
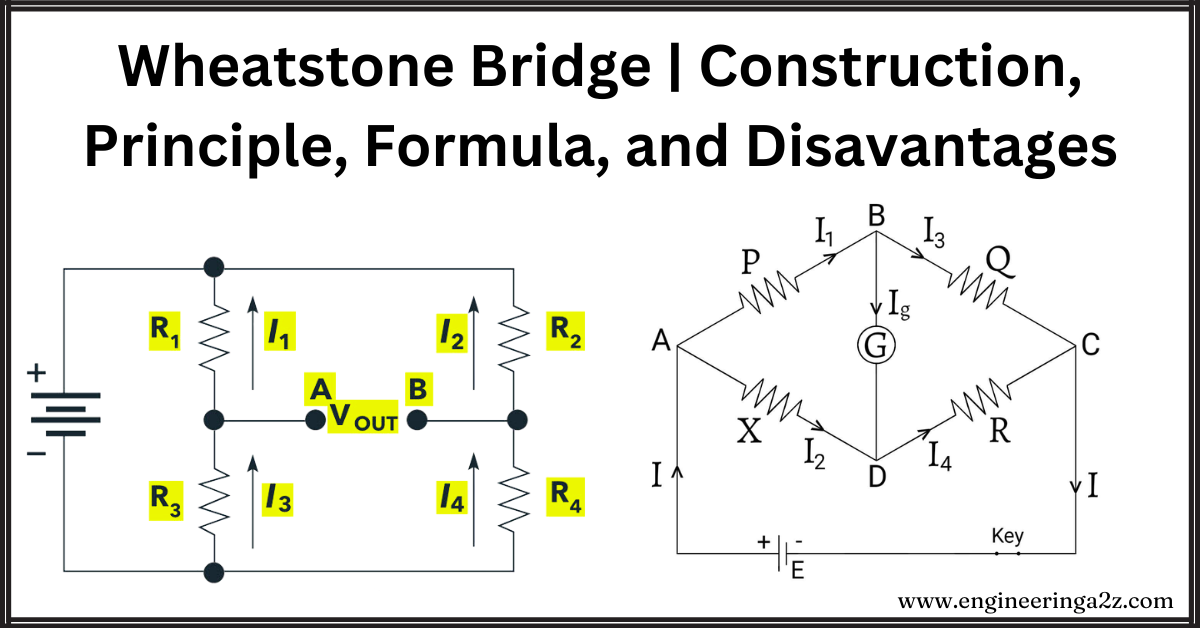
A Wheatstone Bridge is like a team of four players in an electrical game. To build a Wheatstone Bridge, you set up four resistors (P, Q, R, and S) in the shape of a four-sided figure. Imagine it like points A, B, C, and D on the corners. You also add a cell (E) and a key (K1) between A and C, and a sensitive galvanometer (G) and another key (K2) between B and D.
Think of A as having the same potential as the positive side of the cell, and C as having the same potential as the negative side. When K2 is open, P and Q act like buddies in a row (in series), and R and S do the same. But, P and Q (arm ABC) and R and S (arm ADC) team up and connect in a cool way (in parallel).
Now, the galvanometer is like a bridge between ABC and ADC. When everything is perfectly balanced, meaning there’s no deflection in the galvanometer, the ratio of resistances in any two neighboring arms is the same as the ratio of the other two neighboring sides. It’s like finding the perfect match in this electrical balancing act.
Principle of Wheatstone Bridge
The Wheatstone Bridge operates like a cool balancing act. When everything is perfectly balanced, it’s called “null deflection,” meaning the needle of the galvanometer doesn’t move at all. It’s like a no-current, no-movement situation.
But if the balance is off, and there’s a difference in potential, the galvanometer shows a deflection – the needle moves. By adjusting the variable resistor, we play the balancing game until the potential difference becomes zero, reaching the perfect, equilibrium state of the Wheatstone Bridge. It’s like finding the sweet spot where everything stays still and balanced.
Derivation of Wheatstone Bridge
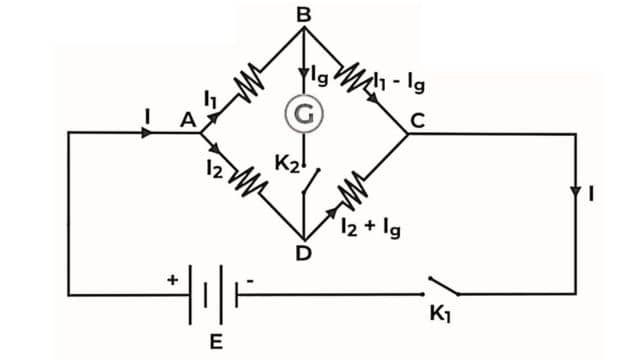
When the Wheatstone Bridge is perfectly balanced, the current through the galvanometer (IG) becomes zero. We have two currents, I1 and I2, flowing through different parts of the bridge. According to Kirchhoff’s law, the total voltage drop around the closed loop (ABDA) is zero, meaning the sum of voltage drops in each part of the loop equals zero.
I1P − I2R = 0
I1 / I2 = R / P
Applying Kirchhoff’s law to the loop CBDC
I1Q − I2S = 0
I1 / I2 = S / Q
Comparing conditions,
R / P = S / Q
P / Q = R / S
This is the formula for the Wheatstone Bridge.
Wheatstone Bridge Formula
Following is the formula used for the Wheatstone bridge:
R = PS / Q
Where,
- R is the unknown resistance
- S is the standard arm of the bridge
- P and Q is the ratio of the arm of the bridge
Example of Wheatstone Bridge
Question: In a Wheatstone’s bridge P = 50Ω, Q = 500Ω and R = 20Ω. If its galvanometer shows zero deflection, then determine the value of resistance S.
Solution: We have the known resistances as:
P = 50 Ω, Q = 500 Ω and R = 20 Ω
For zero deflection in galvanometer, we have the whetstone bridge formula as:
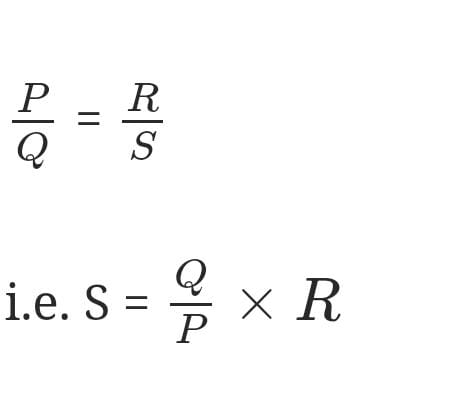
i.e. S = 500 / 50 × 20
S = 200 Ω.
Advantages of Wheatstone Bridge
- Wheatstone’s Bridge helps create a Meter Bridge.
- Its key advantage is the precise measurement of electric resistance without costly tools.
- Can detect tiny changes, even in milliohms.
- Identifying unknown resistance is easy when others are known.
- Useful for measuring strain and pressure.
Disadvantages of Wheatstone Bridge
- Wheatstone’s Bridge impacted by temperature and EMF cells.
- The quality of the galvanometer affects accuracy.
- Fails if not balanced.
- Unsuitable for large resistance measurements.
- High maintenance costs.
Frequently Asked Questions (FAQs)
-
What is Wheatstone Bridge?
The Wheatstone Bridge finds unknown resistance by balancing two parts of its circuit. One side has the mystery resistance. It’s like an electrical balancing act to get accurate measurements.
-
Is Wheatstone Bridge AC or DC?
The Wheatstone Bridge primarily operates with direct current (DC). While it can be adapted for alternating current (AC) in some cases, its classic use involves DC for accurately measuring resistances in electrical circuits.
-
Does the Wheatstone Bridge work with AC?
The Wheatstone Bridge is designed for use with direct current (DC). However, it can be modified or paired with additional components like capacitors and transformers to adapt to alternating current (AC) applications in certain situations.
-
Which type of wire is used in Wheatstone Bridge?
In Wheatstone Bridge, precision is crucial. Constantan wire, known for its stable resistance and low-temperature coefficient, is commonly used. Its consistent properties contribute to accurate resistance measurements, enhancing the bridge’s effectiveness.
Read Also:
