Introduction

A rotating magnetic field is a particular magnetic field created by using coils with multiple electrical phases (like three phases in many cases) and running electrical currents through them. This magnetic field appears to rotate in a circle. You can also make a rotating magnetic field with just one phase of electricity if you use two coils that produce slightly different magnetic fields that are not synchronized.

People use rotating magnetic fields in things like electric motors, generators, and regulators to make these machines work. It’s a fundamental concept in how these devices operate.

Mathematical Analysis of Rotating Magnetic Field

Usually, to create a rotating magnetic field, you’d have to physically spin a magnet or a coil, which requires an external force. However, there’s a clever trick in electrical engineering.

Instead of spinning anything manually, you can achieve a rotating magnetic field effortlessly by using a particular type of electricity called “polyphase AC supply.” This electricity has three separate phases or flows that work together.

Here’s the magic:

1. You have a part in the machine called the “stator,” and you wrap it with wire in a special way, making sure the wire is evenly spread around.
2. Then, you connect this wire to the three-phase AC supply. Now, something incredible happens. As the electricity flows through this wire in a unique pattern, it automatically creates a magnetic field.
3. The coolest part is that this magnetic field doesn’t just sit still; it starts to rotate on its own at a specific speed, which we call the “synchronous speed.” You don’t need any external force to spin it; it just happens because of how the three-phase electricity flows through the wire.

This rotating magnetic field is like a hidden superpower in electrical engineering. It’s the secret sauce behind how things like electric motors and generators can work without you having to turn anything by hand. It’s like nature’s way of making things move without any effort!

Certainly, let’s consider a 3-phase, 2-pole stator with three windings: aa’, bb’, and cc’, spaced 120 degrees apart, and supplied with a 3-phase AC supply. This setup is commonly used in electrical machines like motors and generators. Here’s a breakdown of how it works:

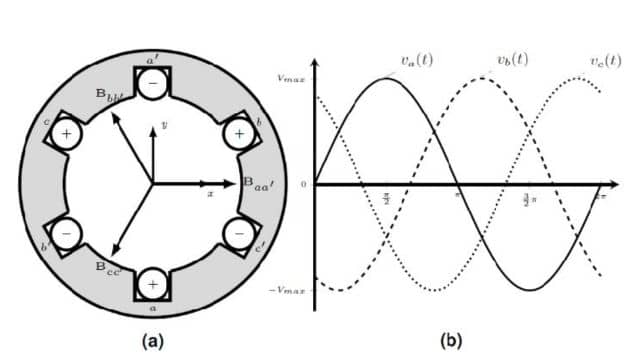
When you have electricity flowing through three different wires, and each wire carries this electricity at slightly different times, it creates a special kind of magnetic force that keeps changing back and forth, just like a swing moving forward and backward.

Now, each of these three magnetic forces, which we call Φ1, Φ2, and Φ3, also goes up and down in strength, just like the waves at the beach. But here’s the trick: each of these magnetic forces reaches its highest and lowest points at different moments in time because they’re not perfectly synchronized. They’re like three friends on a carousel, each sitting one-third apart.

Φ1 = Φm Sin θ
Φ2 = Φm Sin (θ – 120⁰)
Φ3 = Φm Sin (θ – 240⁰)

Where Φm = the maximum value of the flux due to any phase. The waveforms of these fluxes and their phase representation are shown below.

Think of these three magnetic forces, Φ1, Φ2, and Φ3, like three friends working together. When they’re in sync, they create a special effect called a “Rotating Magnetic Field.”

Now, let’s imagine four different moments in time, like snapshots of this magnetic field:

1. At the very beginning (0⁰), it’s like the friends are starting their dance. The magnetic forces haven’t moved much yet, and they’re just getting started.
2. A bit later (60⁰), it’s as if they’ve each taken a step in their dance. The magnetic forces are still coming together but are slightly shifted from where they started.
3. Then, at 120⁰, they’re like three dancers perfectly spaced on the floor. The magnetic forces are working together at full strength, creating the most powerful rotating magnetic field effect.
4. Finally, at 180⁰, it’s like they’ve completed half of their dance. The magnetic forces have moved around halfway in their cycle, but they’re still creating the rotating magnetic field.

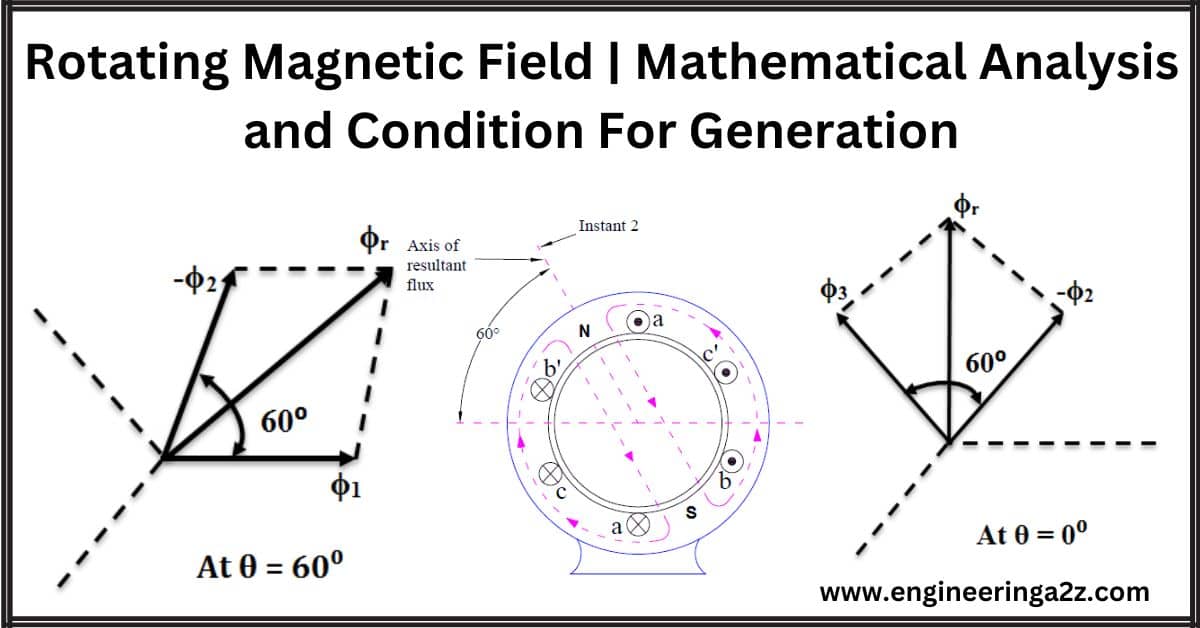
So, when you add up these three magnetic forces at each of these moments, you get the “resultant flux,” Φr. This resultant flux is what makes the rotating magnetic field effect happen, and it changes as these three magnetic forces dance together in sync.

i) When θ = 0⁰ (At point 0) :
At point 0 on the waveform i.e., at 0⁰, the value of Φ1 is,

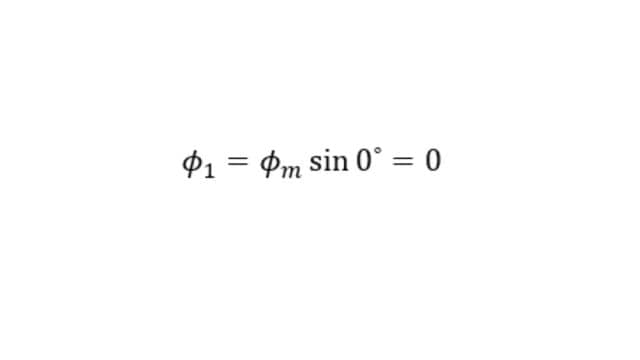
The value of Φ2 is,

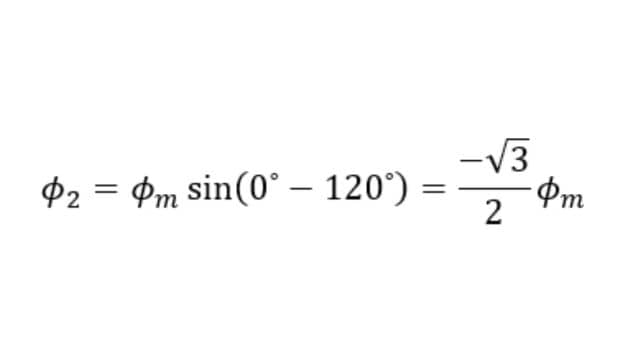
The value of Φ3 is,

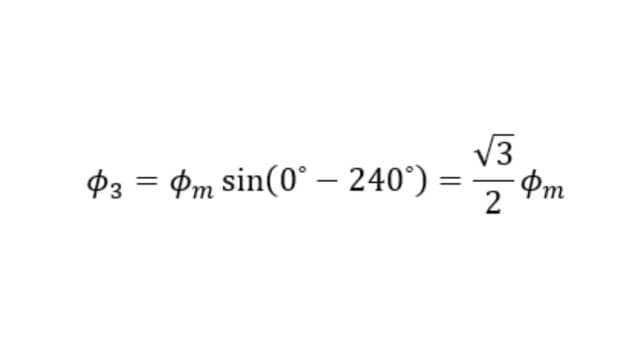
Since Φ1 = 0, the resultant of Φ2 and Φ3 can be found by reversing Φ2 and adding it with Φ3 as shown below.

Rotating Magnetic Field

From the figure Resultant flux Φr,

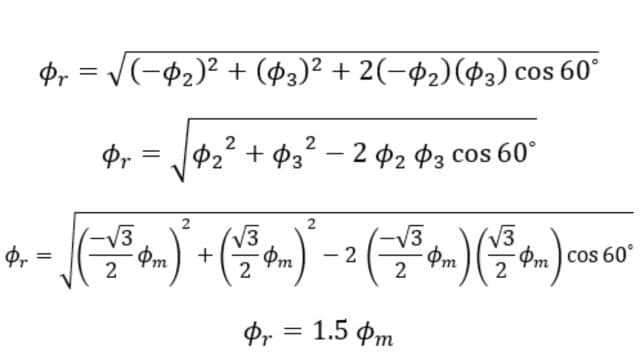
So at 0⁰, the magnitude of resultant flux is 1.5 times the maximum value of individual flux.
ii) When θ = 60⁰ (At point 1) :

At point 1 on the waveform i.e., at 60⁰, the value of Φ1 is,

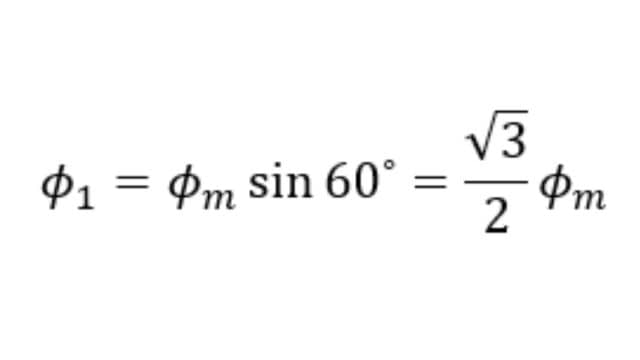
The value of Φ2 is,

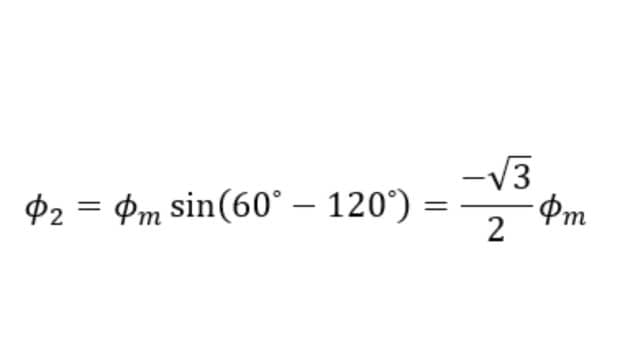
The value of Φ3 is,

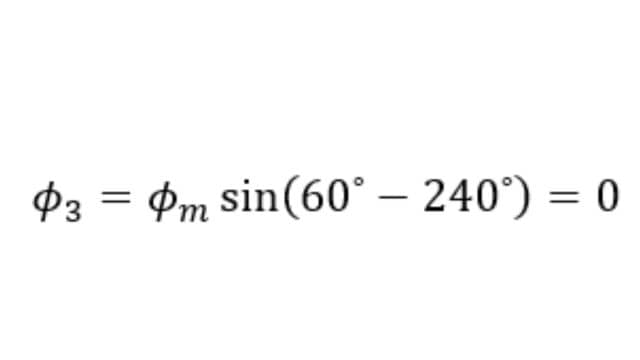
Since Φ3 = 0, the resultant of Φ1 and Φ2 can be found by reversing Φ2 and adding it with Φ1 as shown below.

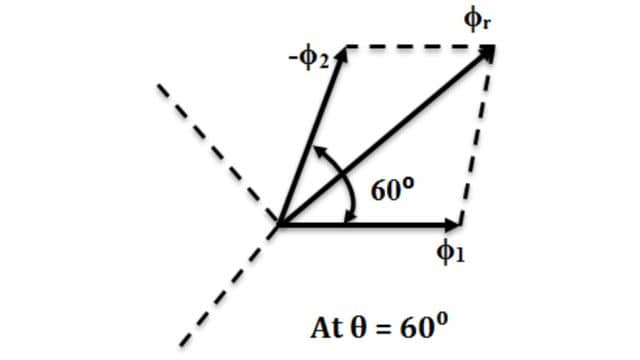
From the figure Resultant flux Φr,

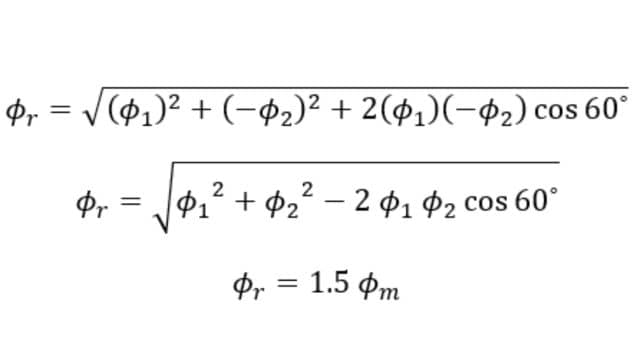
Therefore at 60⁰, the magnitude of resultant flux Φr = 1.5 Φm. Here we can notice that the magnitude of Φr is the same as that of the previous, also the phasor has rotated clockwise through an angle of 60⁰.

iii) When θ = 120⁰ (At point 2) :
At point 2 on the waveform i.e., at 120⁰, the value of Φ1 is,

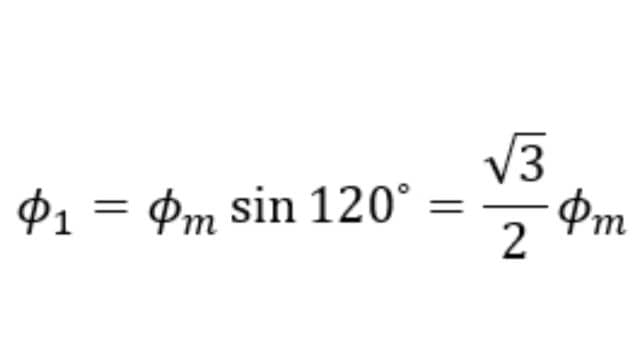
The value of Φ2 is,

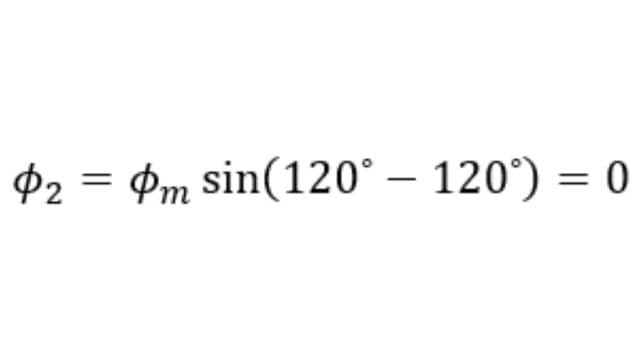
The value of Φ3 is,

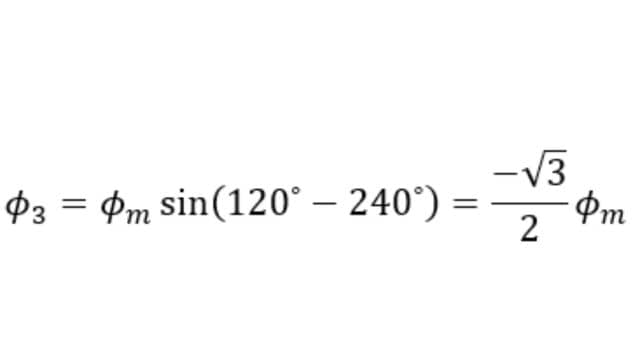
Since Φ2 = 0, the resultant of Φ1 and Φ3 can be found by reversing Φ3 and adding it with Φ1 as shown below.

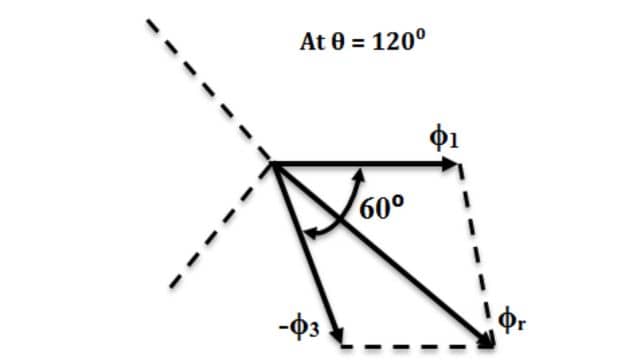
From the figure Resultant flux Φr,

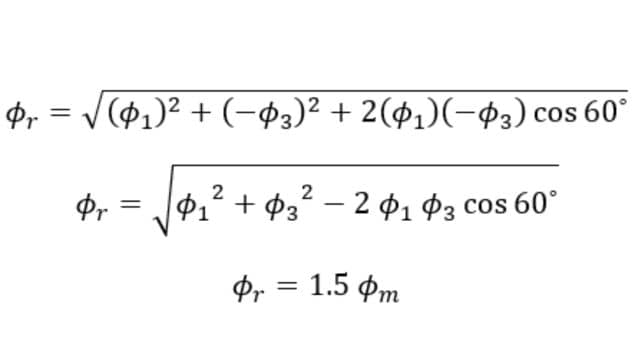
Therefore at 120⁰, the magnitude of resultant flux Φr = 1.5 Φm. Here also, the magnitude of Φr is the same as that at 0⁰ and 60⁰, but the phasor has further rotated clockwise through an angle of 60⁰ or 120⁰ from the start.

iv) When θ = 180⁰ (At point 3) :

At point 3 on the waveform i.e., at 180⁰, the value of Φ1 is,

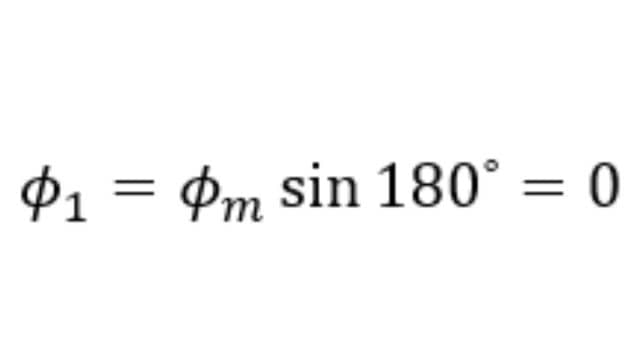
The value of Φ2 is,

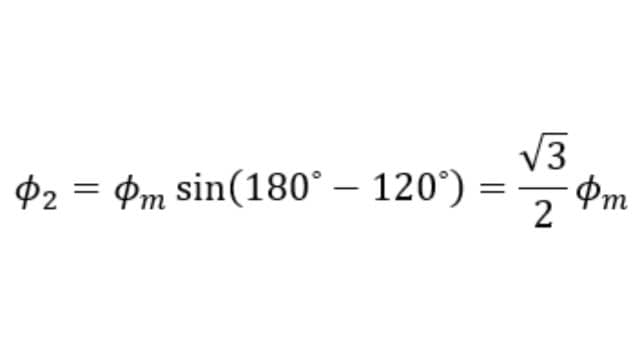
The value of Φ3 is,

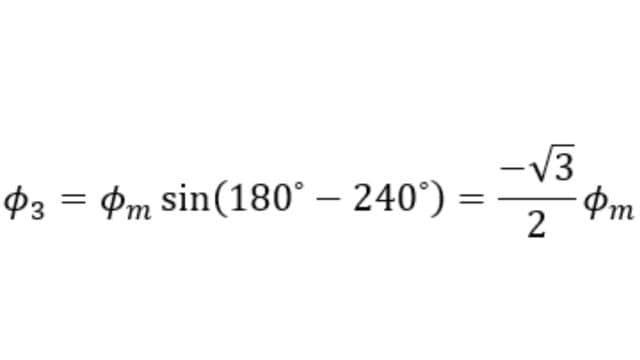
Since Φ1 = 0, the resultant of Φ2 and Φ3 can be found by reversing Φ3 and adding it with Φ2 as shown below.

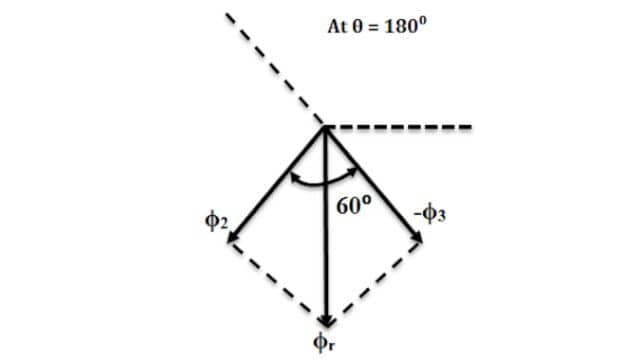
From the figure Resultant flux Φr,

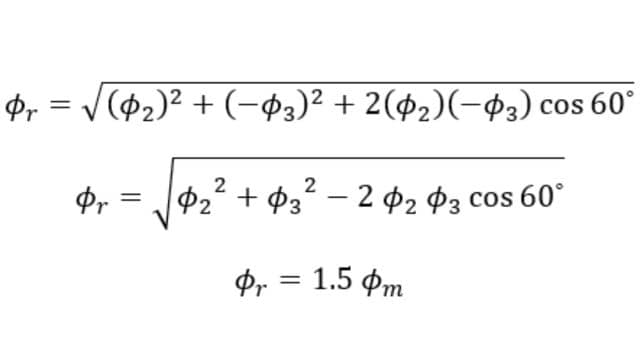
Hence Φr = 1.5 Φm but has rotated clockwise through an additional angle of 60⁰ or 180⁰ from the start.
From the above, it is clear that,

The resultant flux is of constant magnitude and has a value of 1.5 Φm i.e., Φr = 1.5 Φm.

The resultant flux rotates at the synchronous speed, Ns is given by

Ns = 120f/P rpm

Where f = supply frequency and P = number of poles of the stator winding. Therefore, when a 3-phase supply is fed to a 3-phase stator winding, a rotating magnetic field of constant magnitude rotating at synchronous speed is produced.

Condition for Generation of Rotating Magnetic Field

Imagine you have three coils, labeled a, b, and c, and they’re all lined up so their magnetic directions point in the same way. Now, you’re sending electricity through them in a special way. One coil gets a current that starts at its peak, another starts a bit later, and the third starts even later, kind of like they’re taking turns.

Here’s the key: to make a rotating magnetic field, it’s important that the time gap between when these currents start is the same as the gap between the directions of the coils. Think of it like a dance where everyone needs to be in sync.

Now, in the example you mentioned, the currents start at different times, which is like the dancers being out of step. But the coils are all lined up like they’re in a straight line, so there’s no twist or rotation happening. It’s like the dancers are moving, but they’re not making the whole group spin around.

So, because the timing of the currents doesn’t match the way the coils are positioned, you won’t get that cool rotating magnetic field effect. It’s all about making sure both the timing and the arrangement are just right for the magic to happen.

Frequently Asked Questions (FAQs)

Read Also:

• Magnetic Field | Introduction | Effects
• Single Phase Induction Motor | Double Revolving Field Theory
• Tidal Energy | Working, Parts, and Applications
• Quality Systems | Types, Benefits, and Need For Standardization

Read More>>>>