Filter | Single, Double, and Triple Tuned Filters

Design of a Single-Tuned Filter

The single-tuned filters are designed to filter out (usually) characteristic harmonies of a single frequency. The equivalent circuit seen by the harmonic current I_h generated by the converter is shown in Fig. Z_Fh and Z_Sh are the filter and system impedances at the harmonies frequency (hf).

The harmonic current in the filter is given by

I_Fh = I_h |Z_Sh | / |Z_Sh + Z_Fh|

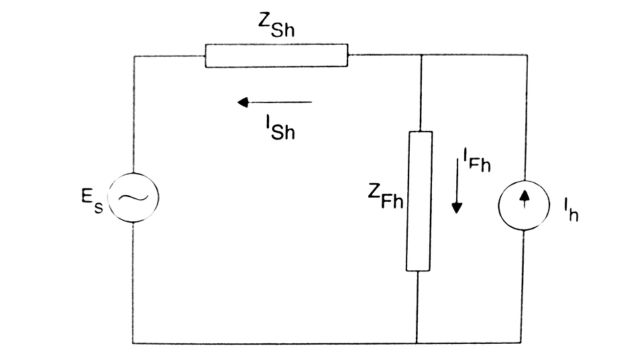
The harmonic voltage at the converter bus is

V_h = I_Fh |Z_Fh| = I_h / |Y_Fh + Y_Sh| = I_h / |Y_h|

The basic objective in designing the filter is to select the filter admittance Y_Fh to minimize V_h or satisfy the constraints on V_h The problem of designing a filter is complicated by the uncertainty about the network admittance (Y_Sh) There are two possible representations of system impedance in the complex plane. These are (a) the impedance angle is limited (see Fig.(a) and (b) the impedance is limited both in angle and impedance. The impedance is assumed to lie in the region shown in Fig. (b) in which R₁, R_2, and θ_m obtained from the system characteristics.

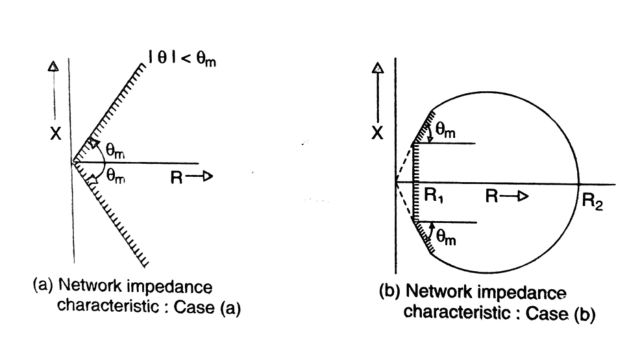
It is to be noted that (a) or (b) reflect the broad assumptions about the nature of system impedance. The assumption (b) requires more knowledge of the system than (a). Having complete information on the network impedance characteristic will result in the economic design of filters and also a realistic assessment of the harmonic distortion of the converter bus voltage.

Although assumption (a) is rather simplistic, it allows a simplified computation of the optimum value of Q. In computing the optimum value of Q, we need to minimize the maximum value of V_h. Since we do not know the exact network impedance (except that its angle is limited), we assume the worst-case scenario for the network admittance that results in maximizing V_h. The optimum value of Q corresponds to the lowest value of the upper limit on V_h.

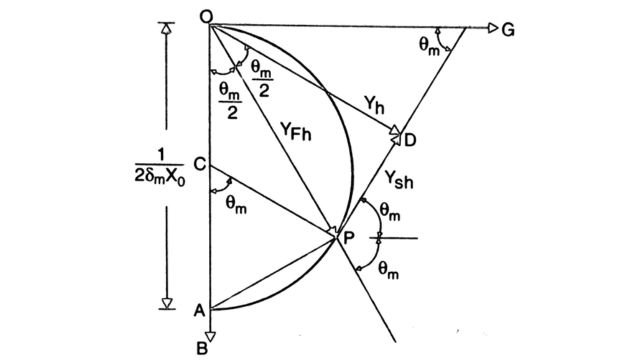
The value of Y_h (the net admittance seen by the converter) is reduced if the detuning parameter 5 is maximum = δm. For a specified δ_m and X₀, the locus of the filter impedance(as Q is varied) is a semicircle in the 4th quadrant of the G-B plane as shown in Fig. The diameter of the circle is 1 / (2δ_m X₀). From the figure’s geometry, It can be seen that minimum Y_h occurs when θ = θ_m. The optimum value of Q can be obtained from game-theoretic analysis. Suppose one selects YFH (OP) arbitrarily (the tip of YFH lying along the semicircle).

In that case, the network can select Y_SH such that the vector Y_h (OD) is perpendicular to PD (the vector Y_SH) and ensure Y_h is a minimum. To maximize the minimum magnitude of Y_h, it is necessary to have PD tangential to the circle at point P. Thus, we select Y_FH to maximize Y_h when the network (viewed as an adversary, not under our control) tries to minimize it.

To compute optimum Q, we note that triangle OPC is isosceles with angle COP = angle CPO = θ_m/2. The angle of the impedance Z_Fh is (90 – θ_m / 2) and we have,

tan(90 – θ_m / 2 ) = Q_opt × (2δ_m) = cot(θ_m /2)

Hence,

Q_opt = cot(θ_m /2) / 2δ_m= 1+cosθ_m / 2δ_msinθ_m

Since |Y_h| = Y_Fh cos(θ_m/2), |Y_Fh | = cos(θ_m/2)/(2δ_mX₀), we can derive the expression for V_h using Eq. We finally get,

V_h = I_h / |Y_Fh +Y_Sh| = 4 δ_m X₀I_h / 1+cosδ_m

Minimum cost tuned filters

The costs of the reactor and the capacitor which make up the tuned filter are dependent on their respective ratings. The rating of the capacitor is given by

S_C = I²_F1X_C1 + I²_FhX₀

where I_F1 is the fundamental frequency current in the tuned filter given by

I_F1 = V₁ . (X_C1 – X_L1) = V₁ / X₀ (h – 1/h) = (hV₁ / (h² – 1) . X₀

In deriving the above equation, the effect of the resistance, R is neglected. V₁ is the fundamental frequency component of the voltage at the filter bus. (Actually, the harmonic components in the bus voltage in steady state, are neglected as filtering of harmonics in the source current supplied to the converter is assumed to be effective). X_C1 = X₀h is the reactance of the capacitor and X_L1 = X₀h is the reactance of the inductor at the fundamental frequency.

The rating of the reactor (S_L) is given by S_L = I²_F1X_L1 + I²_FhX₀

The size of the filter (S) is defined as the reactive power supplied by the capacitor (at the fundamental frequency). Thus, we get

S_C = S + I²_FhX₀

S_L = S / h² + I²_FhX₀

The total cost of the filter (K) is given by

K = S_CU_C + S_LU_L

where U_C and U_L, are the unit costs of the capacitor and inductor, respectively. Substituting Eqs. we get an expression for the total cost as a function of the size of the filter. Since our objective is to determine the optimum size of the filter that will minimize the total cost, we need to express X₀ in terms of the size S. It can be easily shown that

X₀ = N / S, N = V²₁h³ / (h² – 1)²

Substituting Eqns. , we get,

K = AS + BS^-1

where A = U_C + U_L, B = I²_Fh N(U_C +U_L)

It is to be noted that I_Fh is expressed in terms of I_h (the harmonic current injected by the converter)

Since A and B are constants, the cost of the filter is minimum when the size of the filter is minimum given by

S_opt = (B/A)^1/2

The filtering would improve with the increased size of the filter. Hence the choice of the filter size will not be below that given by the above expression.

Design of a High Pass Filter

This is a second-order (damped) filter described earlier. For harmonic frequencies equal to or higher than 17, a second-order high-pass filter is usually provided. By defining the following parameters,

h₀ω=1/√ LC, X₀ = √ L/C, Q = R/X₀

the following values can be chosen

0.5 < Q < 2

h₀ ≤√2h_min

where h_min min is the smallest value of h to be handled by the filter. The choice of h₀ given above implies that the filter impedance at the h_min has decreased approximately to the value of R. The filter impedance is given by Eqn. The reactive power supplied by the filter Q_F is

Q_F = (h₀ / (h_o² – 1))(V₁² / X₀)

In deriving the above, the voltage across the inductor at the fundamental frequency is neglected. It can be shown that the filtering is improved if Q_F, is increased and a higher value of h₀ can be chosen. Hence, it is advantageous to design a high pass filter to exclude six pulse operations. There is no optimum quality factor, Q in the case of high-pass filters. Q is chosen for providing the best performance of the filter over a band of frequencies higher than those covered by tuned filters. The performance of these filters is insensitive to deviations in the frequency or filter parameters.

Double and Triple Tuned Filters

A single-tuned filter can be used to filter one characteristic harmonic (or a non-characteristic harmonic when required). Multiple single-tuned filters are required to filter several (discrete) harmonics. For example, at least two single-tuned filters are required for twelve pulse converters (to filter 11^th and 13^th d harmonics). Since AC filters also provide the required reactive power which is a function of the power flow in the HVDC link, there is a need to arrange the filters into switchable sections (filter banks) which adds to the cost. An alternative is to provide switchable shunt reactors that are switched in at low DC power levels.

This also is a costly option with increased space requirements. Weak AC systems (with low SCR) also impose an upper limit on the size of the filter bank to limit the voltage fluctuations (flicker) caused by the switching of a filter bank. Thus, coordination of the filtering and supplying reactive power considerations dictate the adoption of double and triple-tuned filters. The advantages also include (i) only one inductor (L₁) is subject to full line impulse voltage and (ii) power loss at the fundamental frequency is considerably reduced.

Electrically, neglecting losses, a double-tuned filter is identical to two single-tuned filter branches shown in Fig. (b). Similarly, a lossless triple-tuned filter is identical to three single-tuned filter branches.

The double and triple-tuned filters shown in Figs have a single resister R each. Additional damping resistors can be applied in parallel with reactor L, and/or Ly and L to produce a damped characteristic.

Analysis of a Double-Tuned Filter

The impedance of the filter shown in Fig. (a) (neglecting the effect of R₁) as a function of the complex frequency (s) is given by

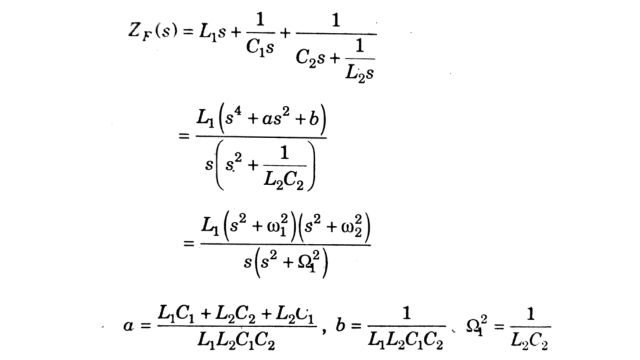
where

The zeros of Z_F(s) lie on the imaginary axis corresponding to the two frequenciesω₁ and ω_2. The poles are also on an imaginary axis corresponding to ω = 0 and ω = Ω. From the properties of the impedance of one-port L-C networks, we can state

0 < ω₁ < Ω₁ < ω₂

Since the double-tuned filter is equivalent to the two single-tuned filters shown in Fig.(a), we can compare the impedances of the two circuits and obtain the following results

L₁ = L_aL_b / (L_a + L_b), L₂ = L_a + L_b, C₁ = C_a + C_b, C₂ = C_aC_b / (C_a + C_b)

From the above, it follows that

L₁L₂ = L_aL_b, C₁C₂ = C_aC_b

The impedance of the double-tuned filter as a function of the frequency is obtained by substituting s = jωh in the expression given in Eq. Note that ω is the fundamental (system) frequency and & is viewed as a continuous variable.

Defining ω_r = 1 / √ L₁C₁ , X₁ = ω₁L₁ = 1 / ω₁C₁ , h_r = ω_r / ω, H₁ = Ω ₁ / ω, X₂ = L₂ = 1 / Ω ₁C₂

We can express the impedance as a function of h as

Z_F (jωh)= jX₁ = (h / h_r – h_r / h) + X₂ / j(h / H₁ – H₁ / h)

J[X₁ . (h² – h²_r ) / (hh_r) – (X₂H₁h) / (h² – H₁²]

To compute ω₁, and ω₂ we equate the RHS of Eq to zero and get the following quadratic equation in h² given below

h⁴ – (h_r² + H₁² + X₂ / X₁ . H₁h_r). h² + h_r²H₁² = 0

The reactive power (Q_F) supplied by the filter is given by

Q_F = V₁² / Z_F1

where Z_F1 = (h_r² – 1) . X₁ / h_r – (X₂H₁) / (H₁² – 1)

Analysis of Triple-Tuned Filters

The impedance of a lossless triple-tuned filter as a function of complex frequency s is given by

Z_F(s) = L₁(s² + ω₁²)(s² + ω₂²)(s² + ω₃²) / (s(s² + Ω₁²)(s² + Ω₂²))

where ω₁, ω₂ and ω₃ are frequencies which have to be filtered Ω₁ and Ω₂ are defined by

Ω₁ = 1 / √L₂C₂ , Ω₂ = 1 / √L₂C₃

The impedances of the filter as a function of ho (h is treated as a continuous variable) are given by

Z_F (jhω) = jX₁ (h / h_r – h_r / h) + X₂ / j (h / H₂ – H₁ / h + X₃ / j(h / H₂ – H₂ / h

where

H₁ = Ω₁ /ω, H_{2} = Ω₂ /ω, h_r = ω_r / ω, ω_r = 1 / √L₁C₁

X₁ = ω₁L₁ = 1 / ω₁C₁, X₂ = Ω₁L₂ = 1 / Ω₁C₂, X₃ = Ω₂L₃ = 1 / Ω₂C₃

To compute ω₁, ω_2, and (the zeroes Z_F) we equate the RHS of Eq. to zero. We finally get a cubic equation in h² given by

h⁶ – a₁h⁴ + a₂h² – a₃ = 0

a₁ = h_r² + H₁² + H₂² + h_r (X₂ /X_{1 .} H₁ + X₃ / X₁. H₁)

a₂ = H₁²H₂² + h_r² (H₁² + H₂²) + h_rH₁H₂ . (X₂ /X₁ . H₂ + X₃ / X₁ . H₁)

a₃ = H₁²H₂²h_r²

h₁ = ω₁ / ω, h₂ = ω₂ / ω, h₃ = ω₃ / ω are the three real roots of Eq. It is easily observed that the product of the real roots is √a_3. This implies that

ω₁ω₂ω₃ = ω_r

we have to select Ω₁ and Ω₂ such that

0 < ω₁ < Ω₁ < ω₂ < Ω₂ < ω₂

Frequently Asked Questions (FAQs)

Read Also:

• Harmonics | Introduction, Generation, and Non – Characteristics
• DC Filters | Criteria, Carrier Frequency, and RI Noise
• Reactive Power Control | Requirement, Sources, and Transients
• DC Breakers | Characteristics, Types, and Applications
• Smoothing Reactor and DC Line | Transient overvoltages, Protection, and Effects

Read More>>>>